The word, Algorithm sounds hi-tech, but in fact it’s very old:
imported into English, from the formerly Latinized as Algorithmi, named for Muḥammad ibn Mūsā al-Khwārizmī.
Al-Khwārizmī was a Persian scholar who produced works in mathematics, astronomy, and geography.
Al-khwārizmī ,would have used tools like this astrolabe, for tracing the path of the stars.

Around 820 CE, Muhammad ibn Mūsā al-khwārizmī was appointed as the astronomer and head of the Library of the House of Wisdom in Baghdad.
It was the equivalent nowadays of receiving both the Nobel Prizes for Literature and Physics at the same time.

Because Al-khwārizmī was the first to treat algebra ,as an independent discipline and introduced the methods of “reduction” and “balancing“
,he has been described as the father of algebra.
(the transposition of subtracted terms to the other side of an equation, that is, the cancellation of like terms on opposite sides of the equation)
The term algebra comes from the title of his book
The Compendious Book on Calculation by Completion and Balancing (specifically the word al-jabr meaning “completion” or “rejoining”).

His name gave rise to the terms Algorism and algorithm.
His name is also the origin of (Spanish) guarismo and of (Portuguese) algarismo, both meaning digit.
However, it is Al-khwārizmī ‘s book which elevates his status to the likes of Euclid, in terms of mathematical prowess.

In it, he presents a systematic solution to linear and quadratic equations, the first person to do so.
Originally, algorithm simply meant what is now called the “Arabic” system of numbers (including zero).
It was the power of Arabic numbers, rather than Latin numerals,
allowed far more complex mathematics to develop, which helped in the study of other areas of science.
Another of his texts, Astronomical Tables, proved to be a turning point in Islamic astronomy.
Prior to Al-khwārizmī, Muslim astronomers had only translated the works of others, but …
“Now they made their own discoveries” Over 100 stars in the sky have Arabic names, including many of the brightest ones…
Only later, algorithm, acquired the more specific sense in mathematics,
of a procedure or set of rules: a writer in 1811 called for an algorithm for establishing theorems.

To this day, algorithm is still just a fancy name for a set of rules.
Ex :If this, then that; if that is true, then do this.
In finance, especially, the word is often shortened to “algo”, which via “algae” evokes a sense of inexorable biological growth.
But perhaps if we thought of algorithms as mere humdrum flowcharts, drawn up by humans,
we’d be better able to see where responsibility really lies if, or when, they go wrong.

The concept of algorithm. has existed for centuries.
The use of the concept can be ascribed to Greek mathematicians, e.g. the sieve of Eratosthenes and Euclid’s algorithm.

Sieve of Eratosthenes: algorithm steps for primes below 121 (including optimization of starting from prime’s square).
In mathematics, the sieve of Eratosthenes is a simple, ancient algorithm for finding all prime numbers up to any given limit.
A partial formalization of what would become the modern notion of algorithm,
began with attempts to solve the Entscheidungs problem(the “decision problem”) posed by David Hilbertin 1928.

Subsequent formalizations were framed as attempts to define “effective calculability” or “effective method”; those formalizations included the Gödel–Herbrand–Kleenerecursive functions of 1930, 1934 and 1935,
Alonzo Church’s lambda calculus of 1936, Emil Post‘s Formulation 1 of 1936, and Alan Turing’s Turing machines of 1936–7 and 1939.

An informal definition could be “a set of rules that precisely defines a sequence of operations.“
which would include all computer programs, including programs that do not perform numeric calculations.
Generally, a program is only an algorithm if it stops eventually.
A prototypical example of an algorithm is the Euclidean algorithm,
to determine the maximum common divisor of two integers; an example (there are others) is described by the flowchart .
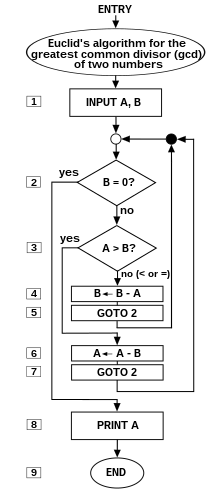
No human being can write fast enough, or long enough, or small enough† ( †”smaller and smaller without limit …you’d be trying to write on molecules, on atoms, on electrons”) to list all members of an innumerably infinite set, by writing out their names, one after another, in some notation.
But humans can do something equally useful, in the case of certain enumerably infinite sets:
They can give explicit instructions for determining the nth member of the set, for arbitrary finite n.
Such instructions are to be given quite explicitly, in a form in which they could be followed by a computing machine, or by a human who is capable of carrying out only very elementary operations on symbols.
An “enumerably infinite set” is one whose elements can be put into one-to-one correspondence with the integers.
Thus, Boolos and Jeffrey are saying that an algorithm implies instructions for a process that “creates” output integers
from an arbitrary “input” integer or integers that, in theory, can be arbitrarily large.

Thus an algorithm can be an algebraic equation such as y = m + n – two arbitrary “input variables” m and n that produce an output y.
But various authors’ attempts to define the notion indicate that the word implies much more than this, something on the order of (for the addition example):
- Precise instructions (in language understood by “the computer”) for a fast, efficient, “good” process that specifies the “moves” of “the computer” (machine or human, equipped with the necessary internally contained information and capabilities)to find, decode, and then process arbitrary input integers/symbols m and n, symbols + and = … and “effectively” produce, in a “reasonable” time, output-integer y at a specified place and in a specified format.

The concept of algorithm is also used to define the notion of decidability. That notion is central for explaining how formal systems come into being starting from a small set of axioms and rules.
In logic, the time that an algorithm requires to complete cannot be measured, as it is not apparently related with our customary physical dimension.
From such uncertainties, that characterize ongoing work, stems the unavailability of a definition of algorithm that suits both concrete (in some sense) and abstract usage of the term.
Algorithms can be expressed in many kinds of notation, including natural languages, pseudocode, flowcharts, drakon-charts, programming languages or control tables(processed by interpreters).

Natural language expressions of algorithms tend to be verbose and ambiguous, and are rarely used for complex or technical algorithms.
- A flowchart is a type of diagram that represents an algorithm, workflow or process.
Pseudocode, flowcharts, drakon-charts and control tables are structured ways to express algorithms that avoid many of the ambiguities common in natural language statements. Programming languages are primarily intended for expressing algorithms in a form that can be executed by a computer, but are often used as a way to define or document algorithms.

- DRAKON algorithm execution is animated by highlighting diagram elements in the running order
There is a wide variety of representations possible and one can express a given Turing machine program as a sequence of machine tables (see more at finite-state machine, state transition table and control table), as flowcharts and drakon-charts (see more at state diagram), or as a form of rudimentary machine code or assembly code called “sets of quadruples” .

Representations of algorithms can be classed into three accepted levels of Turing machine description:
- 1 High-level description
- “…prose to describe an algorithm, ignoring the implementation details. At this level we do not need to mention how the machine manages its tape or head.”
- 2 Implementation description
- “…prose used to define the way the Turing machine uses its head and the way that it stores data on its tape. At this level we do not give details of states or transition function.”
- 3 Formal description
- Most detailed, “lowest level”, gives the Turing machine’s “state table”.
Algorithm design refers to a method or mathematical process for problem solving and engineering algorithms.

The design of algorithms is part of many solution theories of operation research, such as dynamic programming and divide-and-conquer.
Techniques for designing and implementing algorithm designs, are also called algorithm design patterns,
such as the template method pattern, and decorator pattern.

One of the most important aspects of algorithm design is creating an algorithm that has an efficient run-time, also known as its Big O.
Typical steps in development of algorithms:
- Problem definition
- Development of a model
- Specification of algorithm
- Designing an algorithm
- Checking the correctness of algorithm
- Analysis of algorithm
- Implementation of algorithm
- Program testing
- Documentation preparation
